Résultats: Oxyde de métaux de transition et correction de Hubbard
Les atomes de Nickel sont dans un environnement octaédrique. Le Nickel est à l'état d'oxydation +II et devrait donc avoir une configuration électronique de type .
Moment magnétique de NiO
Calcul dans le formalisme DFT
Sans correction de Hubbard, l'optimisation de la densité électronique de NiO conduit aux résulats suivants :
\ N E dE d eps ncg rms rms(c)
DAV: 1 0.170069147592E+03 0.17007E+03 -0.11852E+04 1080 0.143E+03
DAV: 2 -0.206284106087E+02 -0.19070E+03 -0.18041E+03 1060 0.335E+02
DAV: 3 -0.311792171690E+02 -0.10551E+02 -0.10104E+02 1168 0.943E+01
DAV: 4 -0.313299869103E+02 -0.15077E+00 -0.14970E+00 1124 0.119E+01
DAV: 5 -0.313322749937E+02 -0.22881E-02 -0.22782E-02 1148 0.131E+00 0.152E+01
RMM: 6 -0.268644590599E+02 0.44678E+01 -0.14496E+01 1076 0.367E+01 0.434E+00
RMM: 7 -0.268573750866E+02 0.70840E-02 -0.10812E+00 1116 0.632E+00 0.312E+00
RMM: 8 -0.268136432490E+02 0.43732E-01 -0.31912E-01 1074 0.601E+00 0.212E+00
RMM: 9 -0.267887385214E+02 0.24905E-01 -0.15059E-01 1092 0.365E+00 0.106E+00
RMM: 10 -0.267769266674E+02 0.11812E-01 -0.27003E-02 1096 0.222E+00 0.152E-01
RMM: 11 -0.267771627609E+02 -0.23609E-03 -0.13419E-03 1115 0.442E-01 0.240E-01
RMM: 12 -0.267765963561E+02 0.56640E-03 -0.17021E-03 1089 0.358E-01 0.378E-02
RMM: 13 -0.267766040669E+02 -0.77108E-05 -0.46640E-05 1110 0.916E-02 0.254E-02
RMM: 14 -0.267765954812E+02 0.85857E-05 -0.68167E-05 1110 0.743E-02 0.144E-02
RMM: 15 -0.267765943951E+02 0.10861E-05 -0.33016E-06 807 0.214E-02 0.212E-03
RMM: 16 -0.267765943590E+02 0.36181E-07 -0.52743E-07 590 0.625E-03
1 F= -.26776594E+02 E0= -.26776594E+02 d E =0.000000E+00 mag= 0.0000
On remarque que le moment magnétique total est nul. Ceci est cohérent avec l'ordre
magnétique antiferromagnétique de NiO, imposé par la valeur de MAGMOM dans le fichier
INCAR.
Dans le fichier OUTCAR on relève les valeurs de moments magnétiques :
magnetization (x)
# of ion s p d tot
----------------------------------------
1 -0.012 -0.014 1.240 1.214
2 0.012 0.014 -1.240 -1.214
3 0.000 0.000 0.000 0.000
4 0.000 0.000 0.000 0.000
-----------------------------------------
tot 0.000 0.000 0.000 0.000
On voit que le moment magnétique sur chaque atome de nickel est de signe opposé ce qui correspond à l'ordre antiferromagnétique. Les électrons célibataires du Nickel sont des électrons d comme attendu.
Calcul dans le formalisme DFT+U
Si on applique la correction de Hubbard avec U = 8 eV, dans le fichier OUTCAR
on relève les valeurs suivantes de moments magnétiques :
magnetization (x)
# of ion s p d tot
----------------------------------------
1 -0.003 -0.006 1.726 1.717
2 0.003 0.006 -1.726 -1.717
3 0.000 0.000 0.000 0.000
4 0.000 0.000 0.000 0.000
----------------------------------------
tot 0.000 0.000 0.000 0.000
Par rapport au cas sans correction de Hubbard, on voit clairement que l'on a relocalisé les électrons célibataires sur l'atome de Nickel. En effet, on passe de 1.2 électrons à 1.7 électrons. On se rapproche des 2 électrons attendus pour un Ni+II dans une approche complètement ionique.
Ordre magnétique
Comparons les énergies des ordres magnétiques ferromagnétique et antiferromagnétiques.
Il faut donc faire deux calculs en donnant les valeurs de MAGMOM dans le fichier
INCAR qui correspondent à l'ordre souhaité.
Pour l'ordre ferromagnétique, les moments magnétiques sont parallèles :
MAGMOM = 2.0 2.0 0.0 0.0
Pour l'ordre antiferromagnétique, les moments magnétiques sont antiparallèles :
MAGMOM = 2.0 -2.0 0.0 0.0
Résultat pour l'odre antiferromagnétique
= -26.77659436
magnetization (x)
# of ion s p d tot
----------------------------------------
1 -0.012 -0.014 1.240 1.214
2 0.012 0.014 -1.240 -1.214
3 0.000 -0.000 0.000 -0.000
4 -0.000 -0.000 0.000 -0.000
------------------------------------------------
tot -0.000 -0.000 0.000 0.000
Résultat pour l'ordre ferromagnétique
= -26.48718852
magnetization (x)
# of ion s p d tot
----------------------------------------
1 0.011 0.011 0.668 0.691
2 0.011 0.009 0.734 0.754
3 0.017 0.101 0.000 0.119
4 0.017 0.109 0.000 0.126
------------------------------------------------
tot 0.057 0.231 1.402 1.690
Comparaison
Calculons la différence d'énergie entre les deux ordres magnétiques :
= +0.289 eV
L'ordre antiferromagnétique est le plus stable.
Analyse de la DOS de NiO
Calculs dans le formalisme DFT
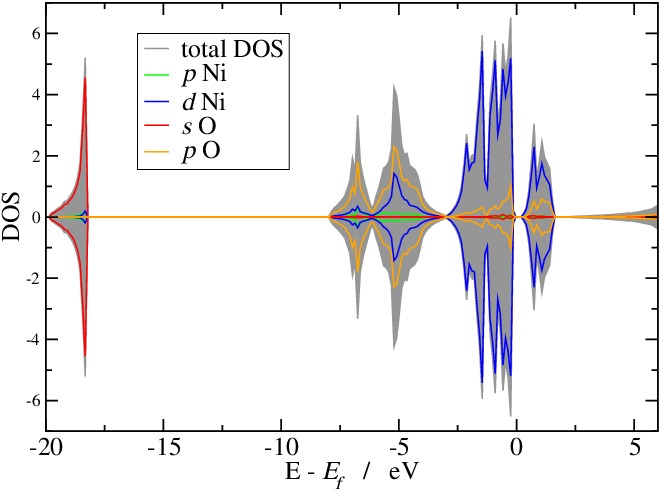
On remarque :
- Absence de gap (0.25 eV)
- Les OA 2s de l'atome d'oxygène sont profondes et peu dispersées.
- La DOS est parfaitement symétrique, donc , ce qui correspond à une situation antiferromagnétique.
Calcul DFT+U, U = 8 eV
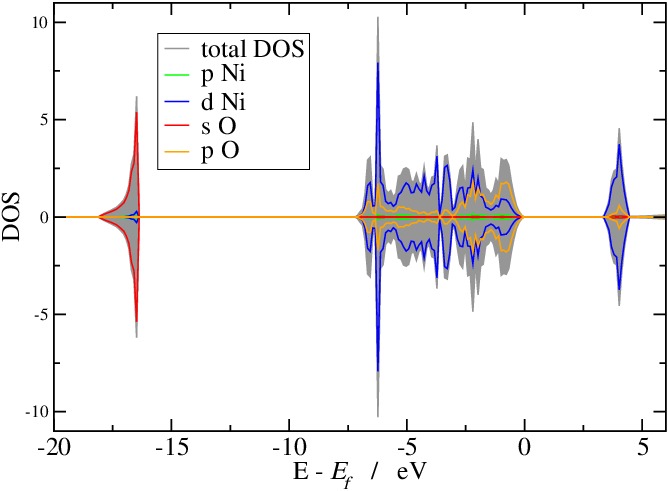
On remarque :
- ouverture du gap 3.4 eV
- Les OA d se sont éloignées du niveau de fermi => effet du U
Compte tenu de l'environement octaédrique des atomes de nickel on peut séparer les contributions des électrons et à la DOS. Sur la figure ci-dessous, la DOS totale est représentée en gris. Les contributions des électrons et d'un atome de nickel sont représentées respectivement en bleu et orange.
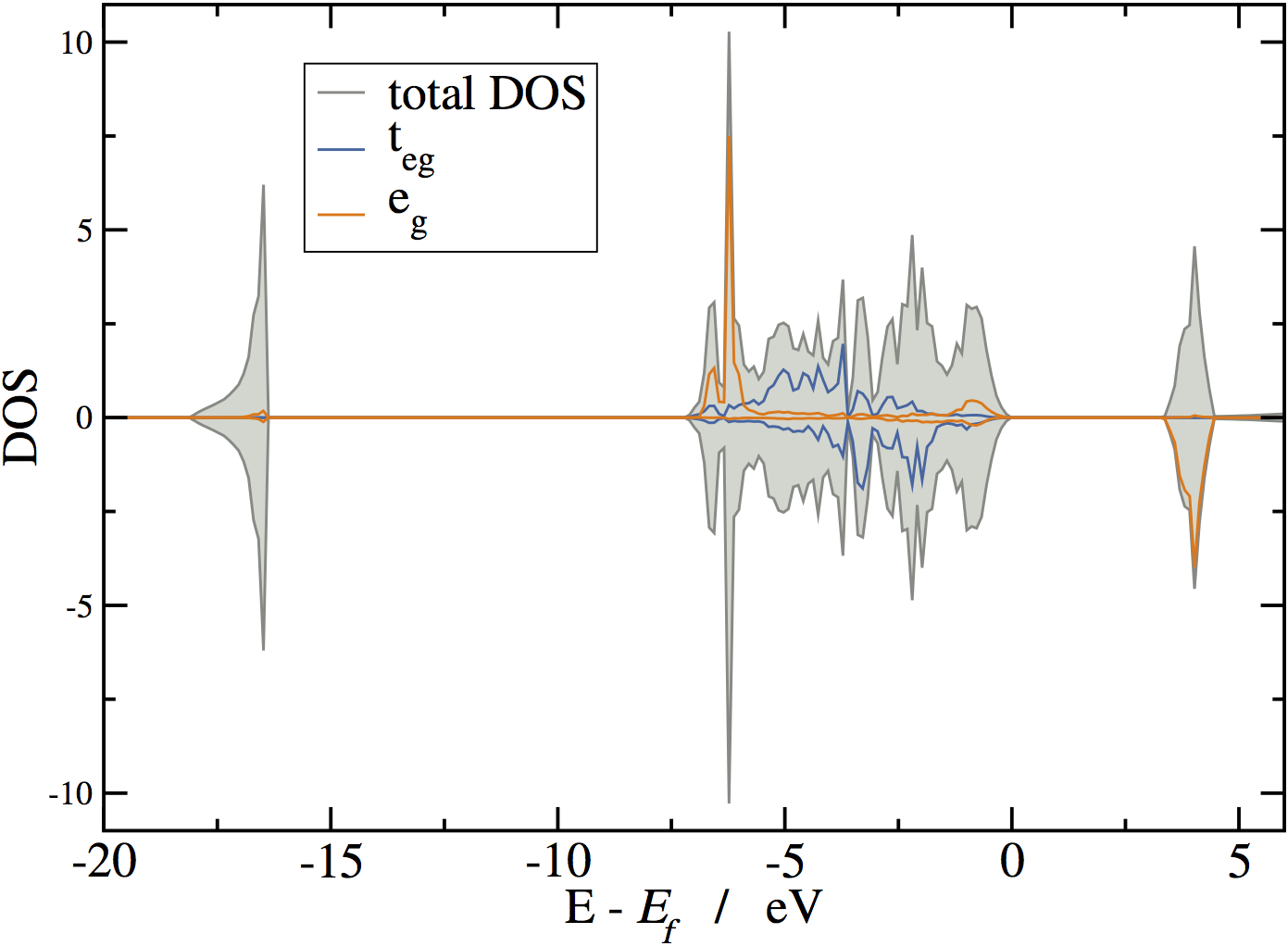
On peut commenter la figure en rapport avec la configuration électronique attendue pour les atomes de nickel : . Les niveaux sont occupés par des électrons up. Ils apparaissent comme vacant pour les électrons down. Les niveaux sont totalement occupés.
Densité d'états en fonction de U
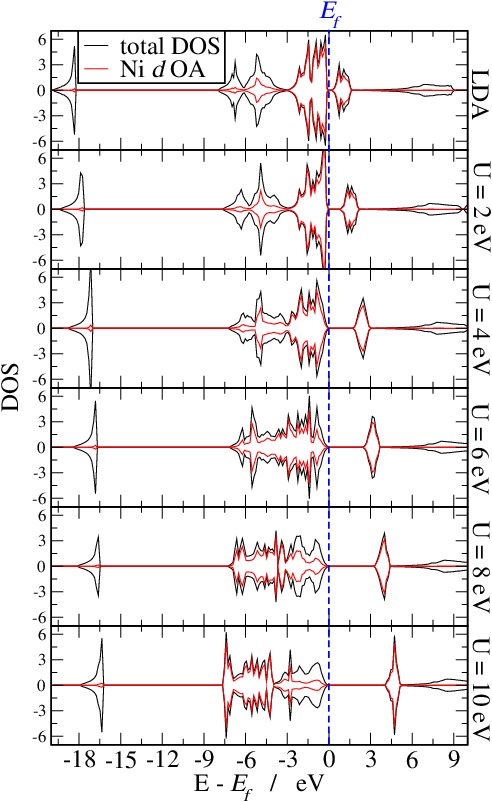
Observations :
- Le gap s'ouvre progressivement
- Les OA 3d du nickel sont progressivement stabilisées sous l'effet du U
Moment magnétique en fonction de U

Observations :
- En fonction de U on augmente progressivement la valeur du moment magnétique.
- Pour une valeur de U comprise entre 7 et 8 eV on retrouve la valeur du moment magnétique expérimentale.
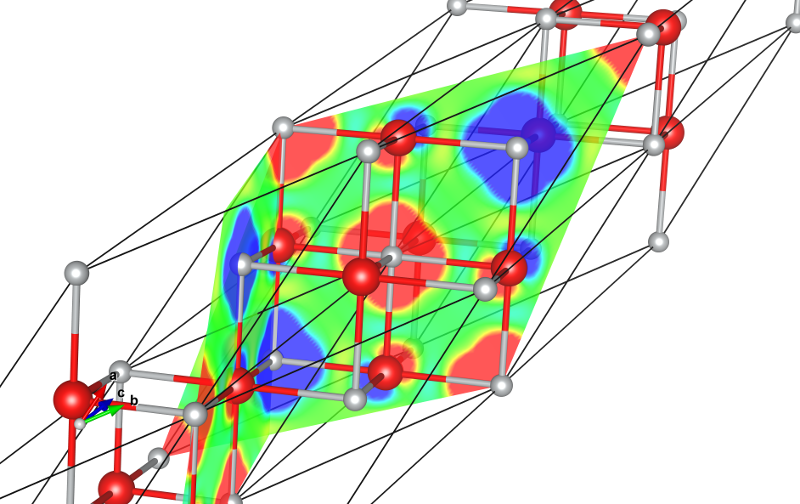
Densité électronique de spin
Les images ci-dessous représentent la densité électronique de spin. On remarque qu'elle change de signe entre deux atomes de Nickel ce qui est représentatif de l'ordre antiferromagnétique. Par ailleurs, la densité de spin se délocalise le long des liaisons Ni-O ce qui est caractéristiques des OA de type .
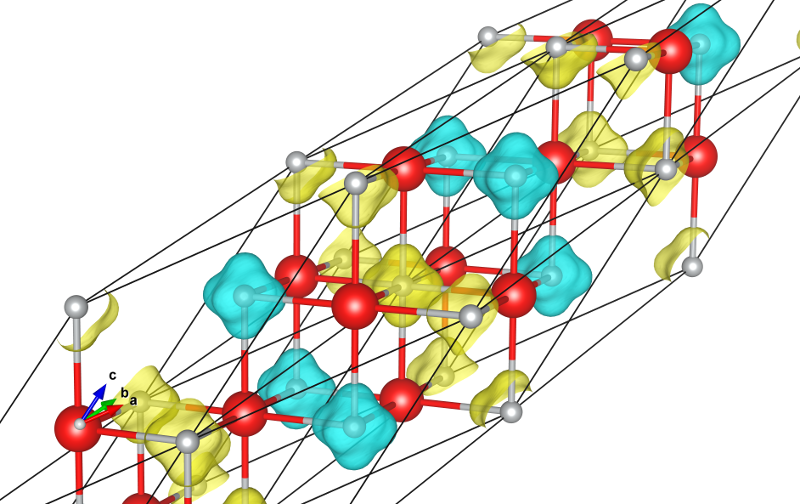
Isodensité de spin. Jaune : valeurs positives, bleu : valeurs négatives