Comment mettre en oeuvre une régression linéaire avec python ?

L'objectif de ce TP est de mettre en pratique le langage python pour réaliser une regression linéaire. L'idée est, dans un premier temps, de reprendre les éléments de base du langage (condition, boucles ...) pour créer un outil qui calcule les paramètres par la méthode des moindres carrés. Dans une deuxième partie les modules spécifiques tels que numpy ou matplotlib seront mis à profit pour réaliser la même opération avec des méthodes existantes.

Introduction

Cahier des charges

Le programme que nous allons écrire devra réaliser les opérations suivantes :

• Lire les valeurs des valeurs de x et y sur le fichier donnees.dat.
• Calculer les paramètres $a$ et $b$ de la régression linéaire par la méthode des moindres carrés et les afficher.
• (bonus) Représenter les points (x,y) et tracer la droite de régression.

Rappels mathématiques

La régression linéaire consiste à chercher les paramètres $a$ et $b$ définissant la droite y=ax+b qui passe au plus près d'un ensemble de points $(x_k,y_k)$. Les paramètres a et b sont déterminés par la méthodes des moindres carrés qui consiste, dans le cas d'une régression linéaire, à minimiser la quantité :

$$Q(a, b) = \sum_{k=1}^N (y_k - a x_k - b)^2$$

Le minimum de $Q(a,b)$ est obtenu lorsque ses dérivées par rapport à $a$ et $b$ sont nulles. Il faut donc résoudre le système à deux équations deux inconnues suivant :

$$\begin{align} & \begin{cases} \displaystyle\frac{\partial Q(a,b)}{\partial a} = 0 \\ \displaystyle\frac{\partial Q(a,b)}{\partial b} = 0 \end{cases} & \Leftrightarrow & & & \begin{cases} \displaystyle -2 \sum_{k=1}^N x_k \left(y_k - a x_k - b\right) = 0 \\ \displaystyle -2 \sum_{k=1}^N \left(y_k - a x_k - b\right) = 0 \end{cases} \end{align}$$

Les solutions de ce système sont :

$$\begin{align} a & = \frac{\displaystyle N \sum_{k=1}^N x_k y_k - \sum_{k=1}^N x_k\sum_{k=1}^N y_k}{\displaystyle N\sum_{k=1}^N x_k^2 - \left(\sum_{k=1}^N x_k\right)^2} & b & = \frac{\displaystyle \sum_{k=1}^N x_k^2 \sum_{k=1}^N y_k - \sum_{k=1}^N x_k\sum_{k=1}^N x_k y_k}{\displaystyle N\sum_{k=1}^N x_k^2 - \left(\sum_{k=1}^N x_k\right)^2} \end{align}$$

Progression

Le programme sera écrit de plusieurs façon différentes.

1. Tous les calculs seront réalisés à la main étape par étape
2. Création d'une fonction qui réalise la régression linéaire
3. Utilisation des array du module NumPy
4. Utilisation des méthodes des modules NumPy/SciPy pour réaliser la régression linéaire
5. (bonus) Utilisation du module matplotlib pour représenter les points et la droite de régression.

Vous pouvez utiliser les deux fichiers ci-dessous contenant un ensemble de données pour réaliser la régression linéaire :

• donnees.dat : 10 valeurs, y = x + 1
• regLinData.dat : 200 valeurs

Programmation

À vous de jouer !

Voici un exemple de graphique que vous pouvez obtenir à la fin de la question 5. :

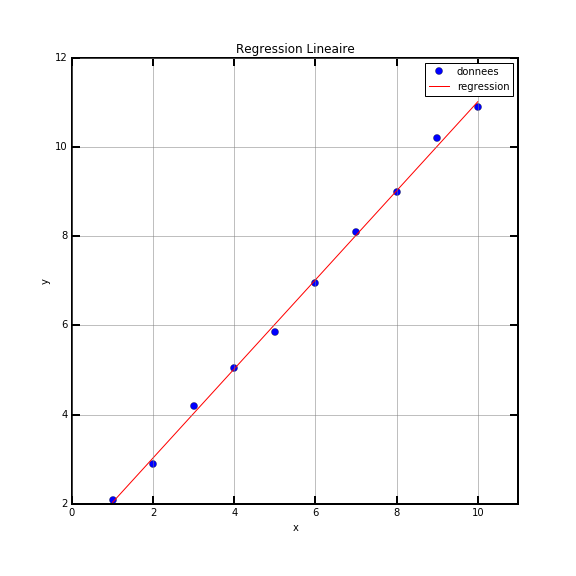
Vous pouvez aussi ajouter le calcul des résidus, notament dans le cas d'un grand nombre de points. On peut alors représenter les données expérimentales et les résidus. On rappelle que les résidus sont les écarts entre les points expérimentaux et le modèle obtenu par la méthode des moindres carrés :

$$R_k = y_k - f(x_k) = y_k (a * x_k + b)$$

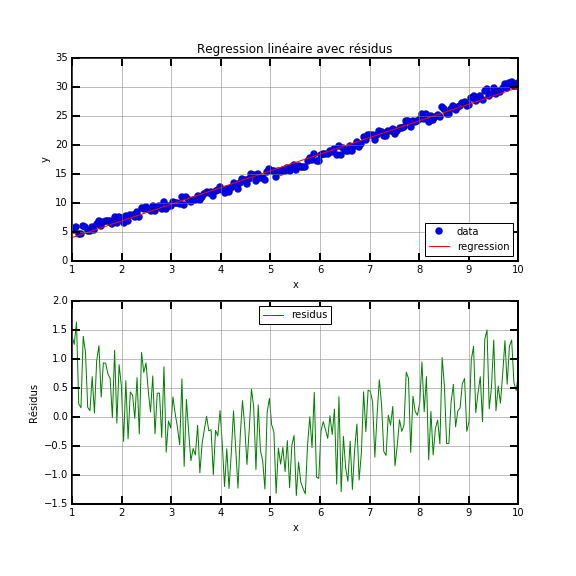
La correction de ce problème est disponnible sous la forme d'un notebook jupyter.