Exercices

Les exercices suivants représentent de petits programmes nécessitant l'utilisation de boucles et de conditions. Ils sont classés par ordre de complexité croissante.

Consignes

Pour chaque exercice choisir des noms de variables adaptés (lisibilité du programme)
Il n'y a jamais trop de commentaires dans un programme, utilisez-les
Essayer d'avoir un programme facile d'utilisation ou facile à utiliser dans un autre contexte
- Création de fonctions
- Documentation
- Création de nouvelles classes
Favoriser les fonctions déjà écrites : elles sont débeuguées et éprouvées. Ne perdez pas du temps à faire ce que quelqu'un d'autre à déjà fait.

Structure générale

Vous pouvez reprendre la structure générale d'un programme présentée lors des séries d'exercices précédentes :

#!/usr/bin/env python
# -*- coding=utf-8 -*-

""" Présentation du code """

def fonction(argument1, argument2):
    """ description de la fonction """

    # instructions de la fonction

    # la fonction retourne éventuellement une valeur
    return "une valeur"

if __name__ == "__main__":
    # instructions à exécuter, par exemple
    #    * lecture des parametres
    #    * appel de la fonction
    fonction()

Énoncés

Écrire un programme qui calcule la factorielle d'un entier naturel.

Rappel :

$\begin{equation*} \begin{cases} n! = 1 \times 2 \times 3 \times \ldots \times n & \forall n \in \mathbb{N}^* \\ n! = 1 & \text{si } n = 0 \end{cases} \end{equation*}$

Écrire un programme qui calcule le produit des $n$ premiers entiers impairs.
Écrire un programme qui calcule la somme des $n$ premiers entiers naturels.
Une population décroit de 40% tous les 3 ans. La population étant considérée négligeable lorsqu'elle est inférieure à 0.1% de sa valeur initiale, au bout de combien d'année l'extinction est-elle atteinte ?
Écrire un programme qui construit une liste de nombres compris entre 0 et 100 puis cherche le minimum et le maximum dans cette liste.
- On peut utiliser la fonction random() du module random pour construire la liste.
- On peut aussi explorer le module numpy.random avec les fonctions random() et randint(), entre autres.
Une marche aléatoire : La marche aléatoire d'un point peut être modélisée de la façon suivante : $\begin{equation*} \vec{r}(t + dt) = \vec{r}(t) + a \hat{\vec{R}} \end{equation*}$ où $a$ désigne l'amplitude du déplacement aléatoire et $\hat{\vec{R}}$ est un vecteur aléatoire dont les composantes sont comprises entre -1 et 1.

Écrire un programme qui met en œuvre une marche aléatoire dans un espace à deux dimensions et affiche à chaque pas de temps les coordonnées du point.

Bonus : Utiliser le module matplotlib pour représenter la trajectoire.
Le nombre $\pi$ peut être calculé par un processus dit de Monte Carlo, mettant en œuvre le tirage de nombres aléatoires. Le principe est le suivant : La probabilité pour qu'un point, de coordonnées $(x, y)$ , $x\in[0,1]$ et $y\in[0,1]$ , choisies aléatoirement, soit dans un cercle de rayon 1 est égale au rapport de l'aire du quart de cercle de rayon 1 et l'aire de ce carré. L'aire du quart de cercle est $\pi / 4$ , l'aire du carré est égale à 1. Le nombre de points appartenant au quart de cercle sur le nombre total de points tirés doit donc converger vers $\pi / 4$ .
- Écrire un programme qui calcule le nombre $\pi$ par cette méthode.
- Visualiser les points avec matplotlib.
Écrire un programme qui calcule l'intégrale d'une fonction par la méthode des trapèze.
Écrire un programme qui calcule l'intégrale d'une fonction par la méthode de Simpson.
[Numpy] Écrire un programme qui met en œuvre le procédé d'orthogonalisation de Gramm-Schmidt dont voici une brève description :

Soit $\vec{u}$ et $\vec{v}$ deux vecteurs quelconques, le vecteur $\vec{v}'$ orthogonal au vecteur $\vec{u}$ est obtenu par : $\begin{equation*} \vec{v}' = \vec{v} - \frac{(\vec{u}.\vec{v})}{||\vec{u}||^2} \vec{u} \end{equation*}$
- Utiliser le module numpy pour travailler avec des vecteurs
- La méthode dot() permet de calculer un produit scalaire
- Le module numpy.linalg contient, entre autre, une méthode norm().

Corrections

ATTENTION : Vous êtes sûr d'avoir suffisamment essayé avant de regarder la correction !!

factorielle d'un entier naturel.

def factorielle(n):
    """ Calcul de factorielle n """

    if n == 0:
        factorielle = 1
    else:
        # initialisation
        factorielle = 1

        # calcul
        for i in range(2, n + 1):
            factorielle *= i

    return factorielle

if __name__ == "__main__":
    # lecture de n
    n = int(input("entrer n : "))
    print("n = ", n)

    # affichage du résultat
    print("{0}! = {1}".format(n, factorielle(n)))

La fonction factorielle est disponible dans le module scipy :

# la fonction factorial est dans le module misc de scipy
>>> from scipy.misc import factorial
>>> factorial(6)
array(720.0)
>>> factorial(3)
arrat(6.0)
# en utilisant n! = gamma(n+1) avec la fonction gamma dans le module 'special'
>>> from scipy.special import gamma
>>> gamma(4)
6.0
>>> gamma(7)
720.0

produit des n premiers entiers impairs

def prog_produit(n):
    """ Calcul du produit des n premiers entiers impairs """

    # initialisation
    produit = 1

    # calcul
    for i in range(3, n + 1):
        if i % 2 == 1:
            produit *= i

    # retour
    return produit

def prog_produit2(n):
    """ Calcul du produit des n premiers entiers impairs """

    # initialisation
    produit = 1

    # calcul
    for i in range(3, n + 1, 2):
        produit *= i

    # retour
    return produit

if __name__ == "__main__":
    # lecture de n
    n = int(input("entrer n : "))
    print("Calcul du produit des ", n, " premiers entiers impairs")
    produit = prog_produit(n)
    print("Résultat = ", produit)

On peut tester la performance d'un algorithme avec le module cProfile :

import cProfile
cProfile.run("prog_produit(100000)")

Ce qui donne :

4 function calls in 0.783 seconds

Ordered by: standard name

ncalls  tottime  percall  cumtime  percall filename:lineno(function)
1    0.783    0.783    0.783    0.783 <ipython-input-13-8309133be728>:1(prog_produit)
1    0.000    0.000    0.783    0.783 <string>:1(<module>)
1    0.000    0.000    0.783    0.783 {built-in method builtins.exec}
1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}

import cProfile
cProfile.run("prog_produit2(100000)")

Ce qui donne :

4 function calls in 0.754 seconds

Ordered by: standard name

ncalls  tottime  percall  cumtime  percall filename:lineno(function)
1    0.754    0.754    0.754    0.754 <ipython-input-13-8309133be728>:16(prog_produit2)
1    0.000    0.000    0.754    0.754 <string>:1(<module>)
1    0.000    0.000    0.754    0.754 {built-in method builtins.exec}
1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}

La sortie de la fonction cProfile.run() indique le temps passé dans chacune des fonctions du programme. On remarque que la version 2 de notre fonction est légèrement plus efficace, en raison du test qui est absent dans celle-ci.

Somme des n premiers entiers naturels

def somme(n):
    """ calcul de la somme des n premiers entiers naturels """
    # initialisation
    somme = 0
    # calcul
    for i in range(n + 1):
        somme += i
    # retour
    return somme

if __name__ == "__main__":
    # lecture de n
    n = int(input("entrer n : "))
    print("Calcul de la somme des ", n," premiers entiers.")
    unesomme = somme(n)
    print("Résultat = ", unesomme)

Le calcul de la somme des premiers entiers peut se faire de façon analytique :

def somme(n):
    """ calcul de la somme des n premiers entiers naturels """
    return n * (n + 1) / 2

Décroissance d'une population

def prog_population():
    """
    Une population est réduite de 40% tous les 3 ans.
    Au bout de combien d'années la population est négligeable
    (inférireure à 0.1% de la population initiale) ?
    """

    # initialisation
    population = 100.0
    an = 0
    perte = .4
    seuil = .1 / 100. * population

    # boucle sur les années
    while population > seuil:
        an += 3
        population *= (1. - perte)
        print(an, population)

    print("Au bout de ", an, " ans, la population est négligeable")

if __name__ == "__main__":
    prog_population()

On peut améliorer cette fonction en ajoutant des arguments. Si on donne une valeur aux arguments dans la définition de la fonction, ils sont optionnels.

def prog_population(population, perte=0.4, periode=1):
    """
    Une population est réduite d'un facteur 'perte' sur une 'periode'.
    Au bout de combien d'années la population est négligeable
    (inférireure à 0.1% de la population initiale) ?

    Args:
        population (float): population initiale
        perte (float): facteur de perte
        periode (int): période en année
    """

    # initialisation
    an = 0
    seuil = .1 / 100. * population

    # boucle sur les années
    while population > seuil:
        an += periode
        population *= (1. - perte)
        print(an, population)

    print("Au bout de ", an, " ans, la population est négligeable")

if __name__ == "__main__":
    prog_population(population=12345, periode=3)

Ici on a passé les arguments dans une syntaxe du type clef=valeur. Dans ce cas, l'ordre des arguments n'a pas d'importance. Comme nous n'avons pas indiqué la valeur de perte lors de l'appel de la fonction, c'est la valeur par défaut qui est utilisée, soit 0.4.

Chercher le minimum et le maximum dans un liste

from random import random
from numpy.random import randint

def minimax(maListe):
    """ Recherche du maximum et du minimum dans maListe """

    # initialisation
    mini = maListe[0]
    maxi = maListe[0]

    for element in maListe:
        # recherche du minimum
        if element < mini:
            mini = element

        # recherche du maximum
        if element > maxi:
            maxi = element

    # retour du résultat
    return mini, maxi

if __name__ == "__main__":
    # nombre de points
    n = int(input("nombre de points : "))
    print("n = ", n)

    # remplissage d'une liste pseudo aleatoire de nombres entre 0 et 100
    maListe = [100. * random() for i in range(n)]
    # ou avec numpy
    # maListe = [randint(0, 100) for i in range(n)]

    mini, maxi = minimax(maListe)
    print("maximum = ", maxi)
    print("minimum = ", mini)

Les fonctions min() et max() existent en python. On peut écrire notre fonction plus simplement suivant :

def minimax2(maListe):
    """ Recherche du maximum et du minimum dans maListe """

    # initialisation
    mini = maListe[0]
    maxi = maListe[0]

    for element in maListe:
        mini = min(mini, element)
        maxi = max(maxi, element)

    # retour du résultat
    return mini, maxi

Bon, on vous a menti ... les fonctions min() et max() renvoient directement le minimum et le maximum dans une liste. Mais vous n'avez pas travaillé pour rien ! L'écriture de cette fonction est formatrice ! :)

>>> from numpy.random import randint
>>> n = 10
>>> maListe = [randint(0, 10) for i in range(n)]
>>> print(maListe)
[53, 65, 12, 38, 38, 91, 31, 46, 44, 50]
>>> max(maListe)
12
>>> min(maListe)
91

Une version simpliste de notre fonction pourrait alors être :

def minimax3(maListe):
    """ Recherche du maximum et du minimum dans maListe """
    return min(maListe), max(maListe)

Regardons ce que nous donne l'analyse des performances avec une liste de 1000000 valeurs :

>>> n = 1000000
>>> maListe = [random() for i in range(n)]
>>> cProfile.run("minimax(maListe)")

Pour la fonction 1

4 function calls in 0.086 seconds

Ordered by: standard name

ncalls  tottime  percall  cumtime  percall filename:lineno(function)
1    0.000    0.000    0.086    0.086 <string>:1(<module>)
1    0.086    0.086    0.086    0.086 minmax.py:9(minimax)
1    0.000    0.000    0.086    0.086 {built-in method builtins.exec}
1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}

Pour la fonction 2

2000004 function calls in 0.744 seconds

Ordered by: standard name

ncalls  tottime  percall  cumtime  percall filename:lineno(function)
1          0.000    0.000    0.744    0.744 <string>:1(<module>)
1          0.332    0.332    0.744    0.744 minmax.py:29(minimax2)
1          0.000    0.000    0.744    0.744 {built-in method builtins.exec}
1000000    0.206    0.000    0.206    0.000 {built-in method builtins.max}
1000000    0.207    0.000    0.207    0.000 {built-in method builtins.min}
1          0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}

On remarque ici un grand nombre d'appels aux fonctions min() et max() ce qui semble être particulièrement inefficace.

Pour la fonction 3

Sans surprise cette fonction est la plus efficace.

6 function calls in 0.051 seconds

Ordered by: standard name

ncalls  tottime  percall  cumtime  percall filename:lineno(function)
1    0.000    0.000    0.051    0.051 <string>:1(<module>)
1    0.000    0.000    0.051    0.051 minmax.py:44(minimax3)
1    0.000    0.000    0.051    0.051 {built-in method builtins.exec}
1    0.026    0.026    0.026    0.026 {built-in method builtins.max}
1    0.025    0.025    0.025    0.025 {built-in method builtins.min}
1    0.000    0.000    0.000    0.000 {method 'disable' of '_lsprof.Profiler' objects}

Une marche aléatoire

from random import random

def marche_aleatoire(npas, amplitude=0.1):
    """
    Marche aléatoire dans un plan 2D

    Args:
        npas (int): nombre de pas
        amplitude (float): amplitude du terme aléatoire
    """
    # liste pour les coordonnées
    x = list()
    y = list()

    # initialisation : condition initiale
    x.append(0.)
    y.append(0.)

    # marche aléatoire
    for i in range(npas):
        wx = 2. * random() - 1.
        wy = 2. * random() - 1.
        x.append(x[i] + amplitude * wx)
        y.append(y[i] + amplitude * wy)

if __name__ == "__main__":
    marche_aleatoire()

Pour faire une représentation graphique de la trajectoire avec matplotlib :

# représentation avec matplotlib
import matplotlib.pyplot as plt

# la trajectoire
plt.plot(x, y, "r-", label="trajectoire")

# points de départ et d'arrivé
plt.plot(x[0], y[0], "go", label="start")
plt.plot(x[-1], y[-1], "bo", label="end")

# format
plt.title("Marche aleatoire dans un plan 2D")
plt.axis("equal")
plt.grid(True)
plt.xlabel("x")
plt.ylabel("y")
plt.legend()
plt.show()

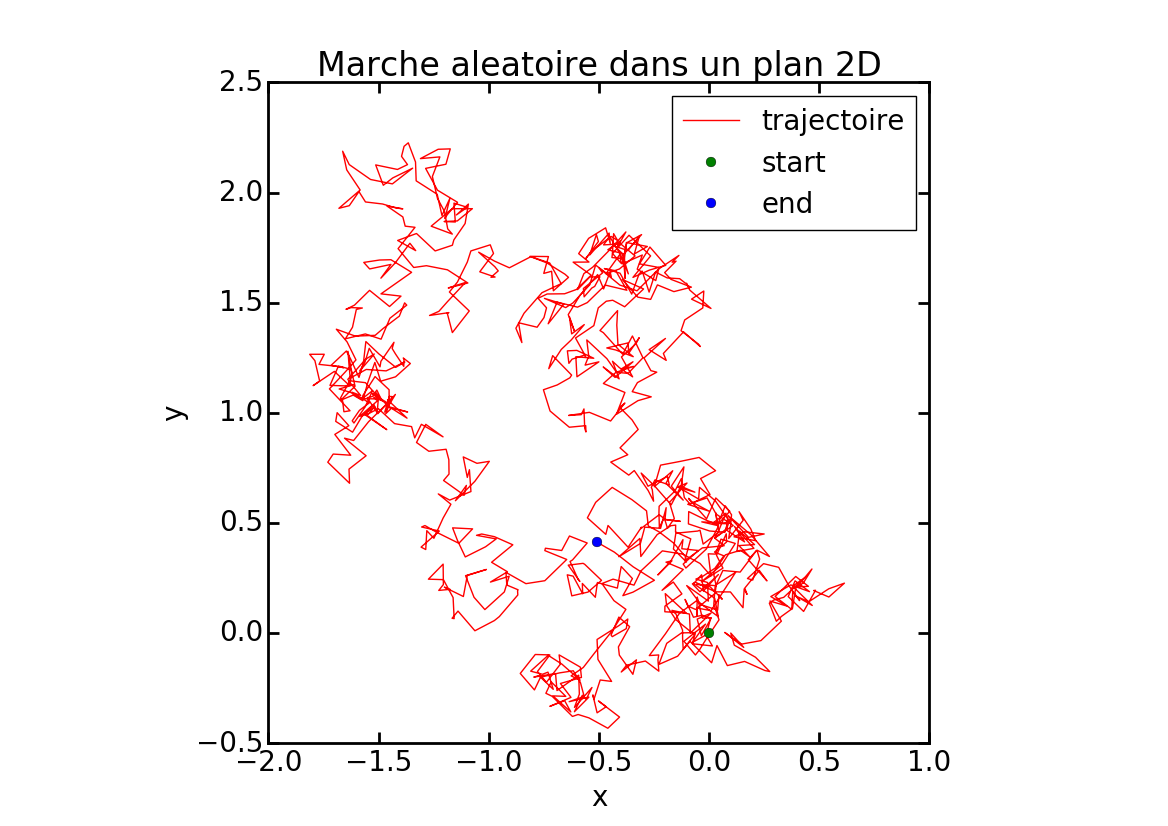
Calcul de $\pi$ par Monte Carlo

import math
from random import random

def prog_pi(ntirage=100):
    """ calcul du nombre pi """

    # initialisation
    n = 0
    xDansCercle = list()
    yDansCercle = list()
    xHorsCercle = list()
    yHorsCercle = list()

    # calcul monte carlo
    for i in range(ntirage):
        x = random()
        y = random()

        if x**2 + y**2 < 1:
            n += 1
            xDansCercle.append(x)
            yDansCercle.append(y)
        else:
            xHorsCercle.append(x)
            yHorsCercle.append(y)

    # affichage des résultats
    piCalcule = 4 * n / ntirage
    print("pi         = ", piCalcule)
    print("% d'erreur = ", (math.pi - piCalcule) / math.pi * 100)

if __name__ == "__main__":
    ntirage = int(input("entrer le nombre de tirage : "))
    print("ntirage = ", ntirage)
    prog_pi(ntirage)

Représentation graphique avec matplotlib.

# representation graphique
import matplotlib.pyplot as plt

plt.figure(figsize=(10, 10))

# points dans le cercle
plt.plot(xDansCercle, yDansCercle, "ro", label="tirages dans le cercle")

# points hors du cercle
plt.plot(xHorsCercle, yHorsCercle, "go", label="tirages hors du cercle")

# cercle
npts = 100
xcercle = [float(xi) / float(npts) for xi in range(npts + 1)]
ycercle = [math.sqrt(1.0 - xi**2) for xi in xcercle]
plt.plot(xcercle, ycercle, "b-", linewidth=3, label="cercle")

# options du graphiques
plt.title("Calcul du nombre pi par monte carlo")
plt.axis("equal")
plt.grid(True)
plt.legend()
plt.xlabel("x")
plt.ylabel("y")

# affichage
plt.show()

Méthode des trapèze

Valeur attendue : $\int_1^3 (x^2 - 3 x - 6) e^{-x} dx = -2.525369$

from math import exp

def trapeze(a, b, npas):
    """ integration par la methode des trapeze """

    # initialisation
    integrale = 0
    pas = (b - a) / npas

    # calcul de l'integrale
    for i in range(npas):
        x = a + i * pas
        integrale += pas * (f(x) + f(x + pas)) / 2

    return integrale

def f(x):
    """ fonction numerique utilisée """
    return (x**2 - 3. * x - 6.) * exp(-x)

if __name__ == "__main__":
    # lecture de l'intervalle
    a = float(input("entrer a : "))
    print("a = ", a)

    b = float(input("entrer b : "))
    print("b = ", b)

    # nombre de segments
    npas = int(input("entrer le nombre de pas : "))
    print("npas = ", npas)

    integrale = trapeze(a, b, npas)
    print("Résultat  = ", integrale)

Remarque : Voir la fonction scipy.integrate.trapz()

Méthode de Simpson

Valeur attendue : $\int_1^3 (x^2 - 3 x - 6) e^{-x} dx = -2.525369$

from math import exp

def simpson(a, b, npas=20):
    """ integration de simpson """

    # initialisation
    integrale = 0.0
    pas = (b - a) / float(npas)
    x = a

    # calcul de l'integrale
    while x < b:
        integrale += pas / 3 * (f(x) + 4 * f(x + pas) + f(x + 2 * pas))
        x += 2 * pas

    return integrale

def f(x):
    """ fonction numérique utilisée """
    return (x**2 - 3 * x - 6) * exp(-x)

if __name__ == "__main__":
    # lecture de l'intervalle
    a = float(input("entrer a : "))
    print("a = ", a)

    b = float(input("entrer b : "))
    print("b = ", b)

    # nombre de pas
    npas = int(input("entrer le nombre de pas : "))
    print("npas = ", npas)

    integrale = simpson(a, b, npas)

    print("Résultat  = ", integrale)

Remarque : Voir la fonction scipy.integrate.simps()

orthogonalisation de Gram-Schimdt

On va se limiter au cas où l'on a seulement deux vecteurs. Rappel de l'expression : $\begin{equation*} \vec{v}' = \vec{v} - \frac{(\vec{u}.\vec{v})}{||\vec{u}||^2} \vec{u} \end{equation*}$

Dans un premier temps nous allons utiliser les listes python.

def schmidt(u, v):
    """
    Procédé d'orthogonalisation de Gram-Schimdt.
    Soit u et v deux vecteurs. On cherche le vecteur vp le plus proche de v
    qui soit rthogonal à u.

    Args :
        u (list): vecteur u
        v (list): vecteur v
    """

    def scal(u, v):
        return sum([ui * vi for ui, vi in zip(u, v)])

    u2 = scal(u, u)

    # calcul du produit scalaire
    scalaire = scal(u, v)
    print("u.v = ", scalaire)

    # orthogonalisation de schmidt
    if scalaire != 0:
        vp = [vi - scalaire / u2 * ui for ui, vi in zip(u, v)]

        # verification
        print("u.vp = ", scal(u, vp))
    else:
        print("u et v sont orthogonaux.")
        vp = v

    return vp

if __name__ == "__main__":
    vp = schmidt(u=[1, 1, 1], v=[1, 2, 3])
    print("vp = ", vp)

Utilisons maintenant les array de numpy :

import numpy as np

def schmidt(u, v):
    """
    Procédé d'orthogonalisation de Gram-Schimdt.
    Soit u et v deux vecteurs. On cherche le vecteur vp le plus proche de v
    qui soit rthogonal à u.

    Args :
        u (list): vecteur u
        v (list): vecteur v
    """

    # Conersion en array numpy
    u = np.array(u)
    v = np.array(v)

    u2 = (u**2).sum()

    # calcul du produit scalaire
    scalaire = np.dot(u, v)
    print("u.v = ", scalaire)

    # orthogonalisation de schmidt
    if scalaire != 0:
        vp = v - scalaire / u2 * u

        # verification
        print("u.vp = ", np.dot(u, vp))
    else:
        print("u et v sont orthogonaux.")
        vp = v

    return vp

if __name__ == "__main__":
    vp = schmidt(u=[1, 1, 1], v=[1, 2, 3])
    print("vp = ", vp)

Premiers programmes

Exercices

Consignes

Structure générale

Énoncés

Corrections

factorielle d'un entier naturel.

produit des n premiers entiers impairs

Somme des n premiers entiers naturels

Décroissance d'une population

Chercher le minimum et le maximum dans un liste

Pour la fonction 1

Pour la fonction 2

Pour la fonction 3

Une marche aléatoire

Calcul de $\pi$ par Monte Carlo

Méthode des trapèze

Méthode de Simpson

orthogonalisation de Gram-Schimdt

results matching ""

No results matching ""

Exercices

Consignes

Structure générale

Énoncés

Corrections

factorielle d'un entier naturel.

produit des n premiers entiers impairs

Somme des n premiers entiers naturels

Décroissance d'une population

Chercher le minimum et le maximum dans un liste

Pour la fonction 1

Pour la fonction 2

Pour la fonction 3

Une marche aléatoire

Calcul de \pi par Monte Carlo

Méthode des trapèze

Méthode de Simpson

orthogonalisation de Gram-Schimdt

results matching ""

No results matching ""

Calcul de $\pi$ par Monte Carlo